Papers Explained Review 12: LLMs for Maths

Table of contents

1. Wizard Math (August 2023)
2. MAmmoTH (September 2023)
3. MetaMath (September 2023)
4. ToRA (September 2023)
5. Math Coder (October 2023)
6. MuggleMath (October 2023)
7. Llemma (October 2023)
8. MuMath (December 2023)
9. MMIQC (January 2024)
10. DeepSeek Math (February 2024)
11. Open Math Instruct 1 (February 2024)
12. Math Orca (February 2024)
13. Math Genie (February 2024)
14. Xwin-Math (March 2024)
15. MuMath Code (May 2024)
16. Numina Math (July 2024)
17. Qwen 2 Math (August 2024)
18. Qwen 2.5 Math (September 2024)
19. Open Math Instruct 2 (October 2024)
20. Math Coder 2 (October 2024)
21. AceMath (December 2024)

Wizard Math

WizardMath: Empowering Mathematical Reasoning for Large Language Models via Reinforced Evol-Instruct

Wizard Math are 7B, 13B and 70B models, created through SFT of Llama 2 on 15K answers re-generated in a step-by-step format using an Alpha version of WizardLM 70B, focusing on the GSM8k and MATH datasets. Additionally, to enhance the model’s ability to adhere to diverse instructions, 1,500 open-domain conversations are sampled from WizardLM’s training data and combined with the math corpus.

To further enhance the model’s capabilities, the Evol-Instruct method is adapted for mathematics, which uses two evolution strategies: downward evolution, which simplifies high-difficulty questions or creates easier questions on different topics, and upward evolution, which increases question complexity by adding constraints, making questions more specific, and requiring deeper reasoning.

The final phase involves Reinforcement Learning from Evol-Instruct Feedback (RLEIF), where the model is refined through reinforcement learning techniques. Two specialized reward models were developed: the Instruction Reward Model (IRM), which assesses the quality of evolved instructions based on definition, precision, and integrity; and the Process-supervised Reward Model (PRM), which ensures the correctness of each step in the problem-solving process.

The models are available at HuggingFace.

Back to Top

MAmmoTH

MAmmoTH: Building Math Generalist Models through Hybrid Instruction Tuning

Firstly MathInstruct dataset is curated by combining high-quality datasets such as GSM8K, MATH, AQuA, Camel, and TheoremQA. GPT-4 is used to supplement the PoT rationales for datasets. GPT-4 is further used to synthesize CoT rationales for questions in TheoremQA and to create question-CoT pairs using Self-Instruct, to address the lack coverage for college-level math knowledge.

Llama-2 and Code Llama including 7B, 13B, 34B, and 70B models are used as the base models to fine tune on MathInstruct for three epochs.

The dataset and models are available at HuggingFace.

Back to Top

MetaMath

MetaMath: Bootstrap Your Own Mathematical Questions for Large Language Models

Meta Math is created by finetuning Llama 2 on the curated Meta Math QA dataset, the curation involves:

• Answer augmentation, where the goal is to enrich the training dataset by generating multiple reasoning paths for each question. This is achieved through few-shot Chain-of-Thought prompting with temperature sampling.
• Question bootstrapping through LLM rephrasing, aims to increase the diversity by generating rephrased versions of existing questions.
• Question bootstrapping by generating questions solvable through backward reasoning. Two specific approaches are employed: Self-Verification (SV) and FOBAR. In the SV method, the question is rewritten into a declarative statement, followed by a backward reasoning question. In the FOBAR method, the answer is directly appended to the question, and the LLM is asked to determine the value of an unknown variable.

The dataset and models are available at HuggingFace.

Back to Top

ToRA

ToRA: A Tool-Integrated Reasoning Agent for Mathematical Problem Solving

ToRA is created by finetuning Llama 2 and CodeLlama on ToRA Corpus, which is curated by collecting interactive tool-use trajectories from popular mathematical datasets, specifically GSM8k and MATH, synthesized using GPT-4.

To encourage diversity in the model’s reasoning steps and reduce improper tool use, output space shaping is applied. This involves generating multiple trajectories for each question and correcting invalid ones by leveraging a teacher model. The corrected and valid trajectories are then used for further model training, expanding the model’s flexibility in exploring different plausible reasoning paths.

The final model is trained on a combined dataset that includes the original ToRA Corpus and additional valid and corrected trajectories. This comprehensive training helps the model perform effectively on mathematical reasoning tasks.

The models are available at HuggingFace.

Back to Top

Math Coder

MathCoder: Seamless Code Integration in LLMs for Enhanced Mathematical Reasoning

The initial dataset (D0) is created by obtaining solutions for the GSM8K and MATH training sets using GPT-4.

Each solution consists of three components: Natural Language (L) for reasoning, Code (C) for execution, and Execution Results (E). This format is called Natural Language, Code, and Execution (LCE) solutions.

The filtered seed data (ensuring that the solutions match the ground truth answers) is used to fine-tune the CodeLlama-34B model, producing the initial MathCoder model, termed MathCoder-Initial.

The initial MathCoder model is used to generate LCE solutions for new problems. The difficulty gap between the GSM8K (grade-school level) and MATH (competition-level) problems is bridged by pairing a GSM8K problem with MATH problem and prompting GPT-4 to generate a new problem of intermediate difficulty.

The new data (D1) is combined with the seed data (D0) to form the MathCodeInstruct dataset. The base Llama-2 and CodeLlama models are fine-tuned using MathCodeInstruct to create the final MathCoder models.

The dataset are available at HuggingFace.

Back to Top

Muggle Math

MuggleMath: Assessing the Impact of Query and Response Augmentation on Math Reasoning

Two new datasets AugGSM8K and AugMATH are created by complicating and diversifying the queries and sampling multiple reasoning paths from GSM8K and MATH.

• For query augmentation, new queries for the GSM8K dataset are generated using GPT-3.5-turbo-0613 and GPT-4–0613. The augmentation process involves five methods: changing specific numbers in the problems, introducing fractions or percentages, combining multiple mathematical concepts, adding conditional statements, and increasing problem complexity.
• Response augmentation is achieved by using GPT-3.5-turbo-0613 and GPT-4–0613 to generate additional reasoning paths. The augmentation process involves using a 1-shot prompt to maintain consistent response formats. The generated responses are filtered using manual rules to exclude unconventional answers, such as excessively long reasoning paths or those lacking final answers.

Then Llama 2 Models are fine tuned on the augmented datasets.

The models are available at HuggingFace. The datasets are available at GitHub.

Back to Top

Llemma

Llemma: An Open Language Model For Mathematics

Llemma are 7B and 34B language models created by continue pretraining Code Llama. 95% of the training mixture is the Proof-Pile-2, 2% from the Pile (with ArXiv removed), and 3% is from the GitHub subset of RedPajama.

The Proof-Pile-2 is a 55B-token dataset with a knowledge cutoff of April 2023 introduced in this work. It is mixture of scientific papers, web data containing mathematics, and mathematical code, with the exception of the Lean proofsteps subset.

• Code: AlgebraicStack is created. It is an 11B-token dataset of source code from 17 languages, spanning numerical, symbolic, and formal math. The dataset consists of filtered code from the Stack, public GitHub repositories, and formal proofstep data.
• Web data: OpenWebMath is a 15B-token dataset of high-quality web pages filtered for mathematical content based on math-related keywords and a classifier-based math score. It preserves mathematical formatting (e.g., LATEX, AsciiMath), and includes additional quality filters (e.g., perplexity, domain, length) and near-deduplication.
• Scientific papers: The ArXiv subset of RedPajama (an open-access reproduction of the LLaMA training dataset).
• General natural language and code data: the Pile is used as a surrogate training dataset.

The models and dataset are available at HuggingFace:

• Llemma 7B, Llemma 34B
• Proof Pile 2

Back to Top

Mu Math

MuMath: Multi-perspective Data Augmentation for Mathematical Reasoning in Large Language Models

MuMath creates a multi-perspective augmentation dataset, combining strengths from tool-free methods, then Llama2 is finetuned on the curated dataset.

Data Reformulation

• Rephrasing: involves rewriting questions and answers while maintaining their original meaning.
• Reorganization: restructures the solutions to make them clearer and more logically organized. The aim is to enhance comprehension by adding explicit instructions, such as “understand the problem” or “define variables”.

Backward-Forward Transformation (BF-Trans)

• FOBAR Approach: involves masking a specific value in a question and reformulating it into a backward reasoning problem. However, this often leads to a forward reasoning process.
• BF-Trans: To improve upon FOBAR, BF-Trans transforms the original question into a backward one and rephrases it into a secondary forward question where the masked value is directly requested.

Question Alteration

• Difficulty Enhancement: Inspired by WizardMath and MuggleMath, this step increases the difficulty of questions by adding constraints or modifying contexts.
• Expression Replacement: This novel method alters arithmetic expressions in solutions to create new equations.

Nested Multi-task Learning

• Integrates auxiliary tasks like summarizing the question and listing the solving plan into the main task of solving mathematical problems.

The artifacts are available at HuggingFace:

• Models
• Dataset

Back to Top

MMIQC

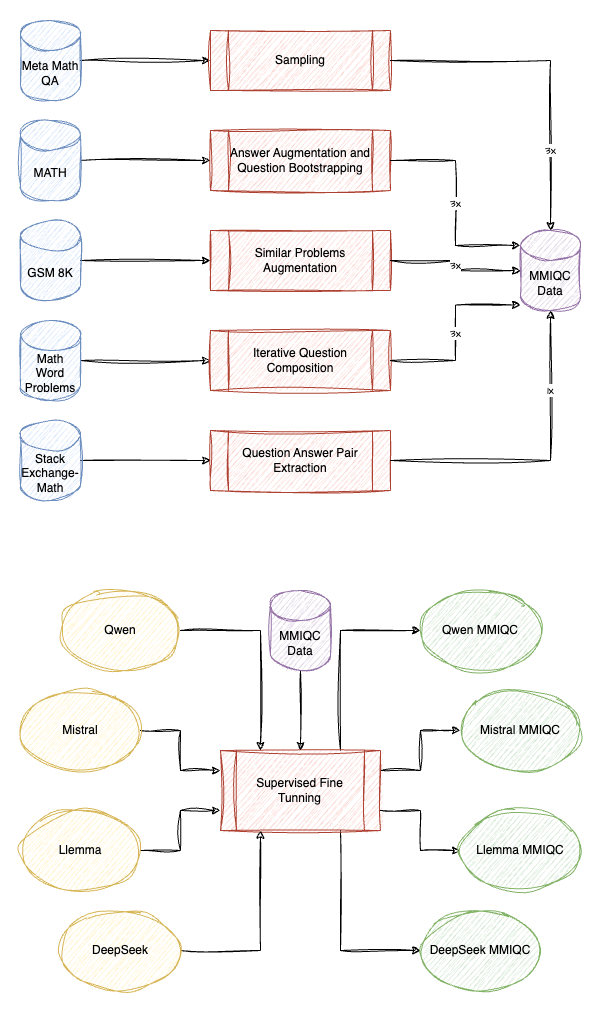
Augmenting Math Word Problems via Iterative Question Composing

The dataset curation methodology for MMIQC is composed of several steps:

• Subset of MetaMathQA: MetaMathQA is constructed by sampling GPT-3.5 for 20 iterations, generating 7 samples for each problem from the MATH and GSM8K datasets. Sampling is restricted to 3 samples per question for MATH and 1 sample per question for GSM8K.
• Answer Augmentation and Question Bootstrapping: This step involves bootstrapping questions using MetaMath techniques. Instead of Few shot prompt, a flexible prompt is used to maintain diversity, and GPT-3.5 performs rejection sampling on both the seed dataset (MATH training set, excluding Asymptote language) and generated questions.
• Similar Problems Augmentation: Inspired by TinyGSM, GPT-3.5 generates 3 similar problems for each problem in the GSM8K training set. GPT-4 then performs rejection sampling to ensure correct solutions.
• Iterative Question Composing: Four rounds of Iterative Question Composing are carried out. GPT-4 generates questions, and GPT-3.5 is used for rejection sampling to refine the quality of questions.
• Mathematics Stack Exchange: Data from Mathematics Stack Exchange is sourced from the OpenWebMath dataset and processed into question-response pairs. Only top-ranked answers are retained for quality.
• Dataset Composition and Shuffling: The final MMIQC dataset includes three repetitions of all subsets (except Mathematics Stack Exchange data). Once combined, the samples are shuffled to prepare the dataset for model fine-tuning.

Mistral, Llemma, DeepSeek and Qwen are then finetuned on the curated dataset.

The dataset is available at HuggingFace.

Back to Top

DeepSeek Math

DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models

The DeepSeekMath Corpus is constructed by iteratively gathering a large-scale mathematical dataset from Common Crawl. Starting with a high-quality seed corpus, OpenWebMath. A fastText model is trained using positive examples from the seed corpus and negative examples from Common Crawl to filter high quality mathematical web data. The final collection consists of 35.5M web pages, totaling 120B tokens.

DeepSeek Coder 1.5 is continued pretrained on this corpus to get DeepSeek Math Base.

A mathematical instruction-tuning dataset is created, covering English and Chinese problems, it includes problems paired with solutions in Chain-of-Thought, Program-of-Thought, and tool-integrated reasoning formats, totaling 776K training examples.

The model undergoes mathematical instruction tuning to get DeepSeek Math-Instruct.

GRPO is introduced as an efficient RL algorithm that extends the traditional Proximal Policy Optimization (PPO) by using the average reward of multiple outputs as a baseline, eliminating the need for a separate value function.

The algorithm is further enhanced with Outcome Supervision (reward at the end of each output) and Process Supervision (reward at each reasoning step) to effectively train the policy model.

The DeepSeekMath-RL model is trained on 144K chain-of-thought-format questions, excluding certain SFT questions.

The models are available at HuggingFace.

Back to Top

Open Math Instruct 1

OpenMathInstruct-1: A 1.8 Million Math Instruction Tuning Dataset

This focuses on creating OpenMathInstruct-1, which contains code-interpreter solutions for GSM8K and MATH generated using Mixtral, then finetunes various open source models to demonstrate the quality of this dataset.

• A few-shot prompting technique is used to synthesize solutions. The prompt includes an instruction , K representative problems with their solutions, and a new question q′. The model generates a solution c′ for q′, which is added to the fine-tuning set if correct. The few-shot prompt consists of 5 examples.
• To address the diversity in MATH, subject-specific prompts are created for seven subjects (algebra, geometry, etc.), with one example from each difficulty level (1 to 5).
• To avoid trivial or shortcut solutions, masked text solutions are used where numbers are replaced with symbols.

The dataset and models are available at HuggingFace.

Back to Top

Math Orca

Orca-Math: Unlocking the potential of SLMs in Grade School Math

Orca-Math is a 7B model created by finetuning Mistral 7B. A seed set of 36,217 math word problems is collected from existing open-source datasets. An agent-based approach is then used to expand this seed set.

An Ask Me Anything agent is the first of these agents, tasked with generating multiple new word problems from each original problem in the seed set. The solutions to these problems are generated using GPT-4 Turbo. A Suggester agent proposes methods to increase the complexity of existing problems, while an Editor agent modifies the problems based on these suggestions.

Additionally, 6,216 problems from the DMath dataset are incorporated.

In the Model Training phase, the initial model training (Iteration #1) involves fine-tuning the Mistral-7B model on the Orca-Math-200K dataset.

The subsequent phase involves Iterative Learning from Positive and Negative Signals. In Dataset Construction Iteration #2, the model fine-tuned in Iteration #1 is used to generate four responses per problem. A preference dataset is created by combining positive and negative solutions for each problem, and the model is trained with Kahneman-Tversky Optimization. The same procedure is repeated in Iteration #3.

The dataset is available at HuggingFace.

Back to Top

Math Genie

MathGenie: Generating Synthetic Data with Question Back-translation for Enhancing Mathematical Reasoning of LLMs

This work curates the MathGenie dataset and then conducts extensive experiments on various pretrained language models, by finetuning them on the curated dataset.

Seed Data:

1. Dtext: This consists of 15,000 math problems with human-annotated solutions from GSM8K and MATH datasets. It serves as the base data for solution augmentation.
2. Dcode: This contains 80,000 samples of math problems with code-integrated solutions and verification rationales, also from GSM8K and MATH. These are used to train a candidate solution generator model.

Candidate Solution Generator (Mcode):

• The Mcode model, a LLaMA-2 70B model trained with Dcode, generates candidate code-integrated solutions for math problems. It has an accuracy of 86.4% on GSM8K and 49.5% on MATH. The model can also verify solutions using the code-integrated rationales.

Iterative Solution Augmentation:

• A new model, Mtext, is created by fine-tuning LLaMA-2 70B on high-quality instructional datasets (OpenOrca and Alpaca-GPT4).
• Mtext is used to iteratively augment the solutions in Dtext. The original solutions, are augmented into new sets creating a final set of augmented solutions. This iterative process ensures that the augmented solutions gradually deviate from the originals, enhancing diversity and reliability.

Question Back-translation:

• To translate augmented solutions (SAug) back into corresponding math problems. A Question Back-translation Model, Mbacktrans, is built by fine-tuning LLaMA-2 70B on reversed pairs of questions and solutions from Dtext.
• The model generates a new set of math problems, QAug, which are more reliable than those generated through direct question augmentation.

Verification-based Solution Filtering:

• Mcode’s verification capability is improved by incorporating code-integrated verification rationales during its training.
• Generate code-integrated solutions for each question in QAug.
• Perform initial filtering based on answer consistency.
• Use Mcode to output verification rationales for each solution; incorrect solutions are discarded.

The models are available at HuggingFace.

Back to Top

Xwin-Math

Common 7B Language Models Already Possess Strong Math Capabilities

Xwin-Math substantially increase the scale of the GSM8K and MATH problems, to 960K and 480K, respectively using the following data augmentation process:

Step 1: Generate a new math question

• The GPT-4 Turbo API generates a brand-new math question based on a reference math question.
• To improve the validity of the new question, three rules are incorporated into the prompt:
• The new question must obey common knowledge.
• It should be solvable independently of the original question.
• It must not include any answer responses.
• Specific formatting requirements for questions and answers are set to tailor them to various target datasets.

Step 2: Verify the question

• The generated questions are validated and refined through attempted solutions.
• By integrating solving and verification steps into a single prompt, the approach consistently elevates the validity of questions across different benchmarks.

Step 3: Generate chain-of-thought (CoT) answers

• For each newly generated question, GPT-4 Turbo produces a chain-of-thought (CoT) answer response.

LLaMA-2 7B/13B/70B/Mistral7B, and math-specific model Llemma-7B are then finetuned on the curated dataset.

The models are available at HuggingFace.

Back to Top

MuMath Code

MuMath-Code: Combining Tool-Use Large Language Models with Multi-perspective Data Augmentation for Mathematical Reasoning

MuMath-Code combines the multi-perspective data augmentation (from MuMath) with code-nested solutions, through a two-stage training strategy.

First stage involves supervised fine-tuning Llama 2 and Code Llama models on MuMath dataset, and the second stages involves fine-tuning on MuMath-Code data, collect as follows:

• Multi-turn Code Generation, Execution, and Reasoning: For each question, proprietary LLMs generate solutions that include at least one block of code. This code is executed by an external interpreter, and the results are appended to the solution.
• Prefix CoT: Before generating code, a thorough natural language analysis (Chain of Thought reasoning) is added to improve model performance. The prompt requests an analysis of the question and the listing of related knowledge points.
• Code Debugging: If the generated code fails, a prompt is added to debug and correct the code, which is repeated until executable code is produced. The failing code and error information are retained to enhance the model’s debugging abilities.
• Pseudo-Answer Guidance Filtering: Majority sampling is used to filter solutions, providing pseudo-answers for questions without reference answers. This improves the correctness and quality of the synthesized solutions.

The artifacts are available at HuggingFace:

• Models
• Dataset

Back to Top

Numina Math

How NuminaMath Won the 1st AIMO Progress Prize

NuminaMath: The largest public dataset in AI4Maths with 860k pairs of competition math problems and solutions

The NuminaMath model is trained in two stages:

• Stage 1: Fine-tune the base model (DeepSeek Math Base) on a large, diverse dataset of natural language math problems and solutions, where each solution is templated with Chain of Thought to facilitate reasoning. The sources of the dataset range from Chinese high school math exercises to US and international mathematics olympiad competition problems.
• Stage 2: Fine-tune the model from Stage 1 on a synthetic dataset of tool-integrated reasoning, where each math problem is decomposed into a sequence of rationales, Python programs, and their outputs. Here, Microsoft’s ToRA format is followed and GPT-4 is used to produce solutions with code execution feedback.

The dataset and models are available at HuggingFace.

Back to Top

Qwen 2 Math

Qwen 2 Math

The base models of Qwen2-Math are initialized with Qwen2–1.5B/7B/72B, and then pretrained on a meticulously designed Mathematics-specific Corpus containing large-scale high-quality mathematical web texts, books, codes, exam questions, and mathematical pre-training data synthesized by Qwen2.

A math-specific reward model is trained based on Qwen2-Math-72B. This dense reward signal is then combined with a binary signal indicating whether the model answered correctly. This combined signal is used as supervision for constructing the SFT data through Rejection Sampling and also in the reinforcement learning with Group Relative Policy Optimization (GRPO) after SFT.

The models are available at HuggingFace.

Back to Top

Qwen 2.5 Math

Qwen 2.5 Math

Qwen 2.5 Math is an upgrade over the Qwen 2 Math series, with extended support to Tool-integrated Reasoning, the notable differences in the methodology include:

• Initialized from Qwen 2.5 (upgrade overQwen 2).
• Additional Synthetic Continued Pretraining Data in generated by Qwen 2 Maths (700B vs 1T tokens).
• The Instruction Tuning Data consists of TIR data

The models are available at HuggingFace.

Back to Top

Open Math Instruct 2

OpenMathInstruct-2: Accelerating AI for Math with Massive Open-Source Instruction Data

This is an upgrade over Open Math Instruct 1 and consists of 14M question-solution pairs (≈ 600K unique questions) generated using Llama 3.1 405B, making it nearly eight times larger than Open Math Instruct , then Llama 3.1 8B and 70B are finetuned to demonstrate the quality of this dataset. Two methods are used for generating synthetic data:

• Solution Augmentation: A few shot prompt is used to generate solutions of the existing questions, onlt the oltuons leading to correct answers are kept.
• Question Solution Augemetation: New questions are generated using a few-shot prompting strategy, followed by solution generation, since the correct answer is not known, majority voting among 32 generations is used.

The experiments show that:

• Solution format matters, with excessively verbose solutions proving detrimental to SFT performance
• Data generated by a strong teacher outperforms equally-sized data generated by a weak student model
• SFT is robust to low-quality solutions, allowing for imprecise data filtering,
• Question diversity is crucial for achieving data scaling gains.

The models and data are available on HuggingFace.

Back to Top

Math Coder 2

MathCoder2: Better Math Reasoning from Continued Pretraining on Model-translated Mathematical Code

This work focuses on curation of the Math Code Pile dataset:

Starting with OpenWebMath,the Mixtral-8x7B-Instruct model is employed to filter out non-mathematical content, reducing the dataset from 13.7B tokens to 4.8B tokens (filtered-OpenWebMath).

A fastText classifier is trained on filtered-OpenWebMath to identify additional math-related content in Common Crawl data. This led to a further round of filtering using the Mixtral-8x7B-Instruct model, resulting in 6.4B tokens (filtered-CC-En-math). Combining filtered-OpenWebMath and filtered-CC-En-math yielded a comprehensive 11.2B-token math-related web dataset.

Some additional sources are further added:

• Synthetic data collected from various open-source repositories on Hugging Face, including datasets such as Education-College-Students and synthetic math books from the Matrix dataset.
• Code data is gathered from the StarCoderData dataset, particularly from Python and Jupyter files that import math-related packages (e.g., sympy, scipy, statistics). The numpy package was excluded to avoid non-mathematical contexts.
• 8,000 PDFs of math textbooks are collected from online sources, focusing on titles with keywords like algebra, geometry, and probability. The PDFs are converted into markdown format using the Nougat tool for easier integration into the training pipeline.

Reasoning steps are extracted from pretraining data and converted into corresponding Python code snippets:

• The Llama-3.1–70B-Instruct model is prompted to extract LaTeX expressions denoting complex computations, their conditions, and expected results.
• A mathematical reasoning step is formed by combining conditions, expressions, and results.
• The model then generates Python code snippets to capture the reasoning behind these steps.
• The generated code snippets are executed, and only those that produced correct outputs were retained. This ensured high-quality, reliable code data.

Llama 3, DeepSeekMath, Mistral, Code-Llama are then continued pretrained on this Math Code Pile dataset, resulting into MathCoder 2 Models, MathCoder2-Llama-3 and MathCoder2-DeepSeekMath are then further fine tuned using the NuminaMath Approach.

The Math Code Pile dataset and the continued pretrained models are available at HuggingFace.

Back to Top

AceMath

AceMath: Advancing Frontier Math Reasoning with Post-Training and Reward Modeling

To Train AceMath, prompts are collected from a diverse range of open-source datasets:

• General domain: ShareGPT, SlimOrca, EvolInstruct, GPTeacher, AlpacaGPT4, and UltraInteract.
• Coding domain: Magicoder, Wizard-Coder, GlaiveCodeAssistant, and CodeSFT.
• Math domain: NuminaMath, OrcaMathWordProblems, MathInstruct, MetaMathQA, and synthetic data.

GPT-4o-mini (2024–0718) is used to generate responses for collected prompts in coding and general domains. Qwen2.5-Math-72B-Instruct is used for generating responses to math prompts.

Synthetic Prompt Generation involves two key steps: 1) leveraging diverse seed prompts to inspire a powerful instruct model to generate entirely new, potentially more challenging or uncommon prompts, and 2) ensuring that the generated prompts are solvable, as unsolvable prompts can lead to incorrect answers, which may degrade performance when used for training.

In-breadth evolution is applied for generating more rare prompts and in-depth evolution for generating more challenging ones using GPT-4o-mini using Numina Math dataset. Two responses per prompt are generated using GPT-4o-mini and answers consistent across both responses are considered potentially correct. Finally, these answers are compared with those from Qwen 2.5-Math-72B-Instruct, and matched final answers are selected as high-quality solutions for training.

SFT is done in two stages on Qwen 2.5-Math models.

• In stage-1, the model is trained on a large dataset specifically curated for code and math SFT tasks.
• Stage-2 expands the scope by incorporating a balanced mix of code, math, and other general SFT data.

Back to Top

References

• WizardMath: Empowering Mathematical Reasoning for Large Language Models via Reinforced Evol-Instruct
• MAmmoTH: Building Math Generalist Models through Hybrid Instruction Tuning
• MetaMath: Bootstrap Your Own Mathematical Questions for Large Language Models
• ToRA: A Tool-Integrated Reasoning Agent for Mathematical Problem Solving
• MathCoder: Seamless Code Integration in LLMs for Enhanced Mathematical Reasoning
• MuggleMath: Assessing the Impact of Query and Response Augmentation on Math Reasoning
• Llemma: An Open Language Model For Mathematics
• MuMath: Multi-perspective Data Augmentation for Mathematical Reasoning in Large Language Models
• Augmenting Math Word Problems via Iterative Question Composing
• DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models
• OpenMathInstruct-1: A 1.8 Million Math Instruction Tuning Dataset
• Orca-Math: Unlocking the potential of SLMs in Grade School Math
• MathGenie: Generating Synthetic Data with Question Back-translation for Enhancing Mathematical Reasoning of LLMs
• Common 7B Language Models Already Possess Strong Math Capabilities
• MuMath-Code: Combining Tool-Use Large Language Models with Multi-perspective Data Augmentation for Mathematical Reasoning
• How NuminaMath Won the 1st AIMO Progress Prize
• NuminaMath: The largest public dataset in AI4Maths with 860k pairs of competition math problems and solutions
• Qwen 2 Math
• Qwen 2.5 Math
• OpenMathInstruct-2: Accelerating AI for Math with Massive Open-Source Instruction Data
• MathCoder2: Better Math Reasoning from Continued Pretraining on Model-translated Mathematical Code
• AceMath: Advancing Frontier Math Reasoning with Post-Training and Reward Modeling

Hungry for more insights?

Don’t miss out on exploring other fascinating threads in this series. Simply click here and uncover the state-of-the-art research!

Do Subscribe for weekly updates!!