Papers Explained Review 10: Normalization Layers

Table of Contents
- Batch Normalization
- Layer Normalization
- Instance Normalization
- Group Normalization
- Weight Standardization
- Batch-Channel Normalization
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers as LBatch Normalization
Batch Normalization was first discussed in the paper Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
They define Internal Covariate Shift as the change in the distribution of network activations due to the change in network parameters during training. This adversely affects training speed because the later layers have to adapt to the shifted distribution.
They proposed that by whitening the inputs to each layer,we would take a step towards achieving the fixed distributions of inputs that would remove the ill effects of the internal covariate shift.
Whitening is linearly transforming inputs to have zero mean, unit variance, and be uncorrelated.
The paper introduces Batch Normalization as follows:
Normalize each feature independently to have zero mean and unit variance:
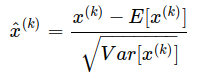
where x=(x(1)…x(d)) is the d-dimensional input.
The estimates of mean and variance are from the mini-batch for normalization; instead of calculating the mean and variance across the whole dataset.
Normalizing each feature to zero mean and unit variance could affect what the layer can represent. To overcome this each feature is scaled and shifted by two trained parameters.

where y(k) is the output of the batch normalization layer.
An exponential moving average of mean and variance is calculated during the training phase and is then used during inference.
class BatchNormalization(L.Layer):
def __init__(self, eps=1e-5, momentum=0.1, **kwargs):
super().__init__(**kwargs)
self.eps = eps
self.momentum = momentum
def build(self, input_shape):
self.exp_mean = self.add_weight(shape=input_shape[-1], initializer='zeros', trainable=False)
self.exp_var = self.add_weight(shape=input_shape[-1], initializer='ones', trainable=False)
self.scale = self.add_weight(shape=input_shape[-1], initializer='zeros', trainable=True)
self.shift = self.add_weight(shape=input_shape[-1], initializer='ones', trainable=True)
def call(self, x):
x_shape = x.shape
batch_size = x_shape[0]
channels = x.shape[-1]
x = tf.reshape(x, (batch_size, -1, channels))
mean = tf.reduce_mean(x, [0, 1])
mean_x2 = tf.reduce_mean((x ** 2), [0, 1])
var = mean_x2 - mean ** 2
self.exp_mean = (1 - self.momentum) * self.exp_mean + self.momentum * mean
self.exp_var = (1 - self.momentum) * self.exp_var + self.momentum * var
mean = self.exp_mean
var = self.exp_var
x_norm = (x - tf.reshape(mean, (1, 1, -1))) / tf.reshape(tf.sqrt(var + self.eps), (1, 1, -1))
x_norm = tf.reshape(self.scale, (1, 1, -1)) * x_norm +tf.reshape(self.shift, (1, 1, -1))
return tf.reshape(x_norm, x_shape) Layer Normalization
Layer normalization, introduced in the paper Layer Normalization is a simpler normalization method that is generally used for NLP tasks but works on a wider range of settings.

class LayerNormalization(L.Layer):
def __init__(self, eps=1e-5, **kwargs):
super().__init__(**kwargs)
self.eps = eps
def build(self, input_shape):
self.gain = self.add_weight(shape=input_shape, initializer='zeros', trainable=True)
self.bias = self.add_weight(shape=input_shape, initializer='ones', trainable=True)
def call(self, x):
normalized_shape = x.shape[1:]
dims = [-(i + 1) for i in range(len(normalized_shape))]
mean = tf.reduce_mean(x, dims, keepdims=True)
mean_x2 = tf.reduce_mean((x**2), dims, keepdims=True)
var = mean_x2 - mean ** 2
x_norm = (x - mean) / tf.sqrt(var + self.eps)
x_norm = self.gain * x_norm + self.bias
return x_normInstance Normalization
Instance normalization was introduced in the paper Instance Normalization: The Missing Ingredient for Fast Stylization to improve style transfer.

class InstanceNormalization(L.Layer):
def __init__(self, eps=1e-5, **kwargs):
super().__init__(**kwargs)
self.eps = eps
def build(self, input_shape):
self.scale = self.add_weight(shape=input_shape[-1], initializer='zeros', trainable=True)
self.shift = self.add_weight(shape=input_shape[-1], initializer='ones', trainable=True)
def call(self, x):
x_shape = x.shape
batch_size = x_shape[0]
channels = x.shape[-1]
x = tf.reshape(x, (batch_size, -1, channels))
mean = tf.reduce_mean(x, [1], keepdims=True)
mean_x2 = tf.reduce_mean((x ** 2), [1], keepdims=True)
var = mean_x2 - mean ** 2
x_norm = (x - mean) / tf.sqrt(var + self.eps)
x_norm = tf.reshape(self.scale, (1, 1, -1)) * x_norm +tf.reshape(self.shift, (1, 1, -1))
return tf.reshape(x_norm, x_shape) Group Normalization
Batch Normalization works well for large enough batch sizes but not well for small batch sizes, because it normalizes over the batch. Training large models with large batch sizes is not possible due to the memory capacity of the devices.
Group Normalization introduced in the paper Group Normalization, normalizes a set of features together as a group. This is based on the observation that classical features such as SIFT and HOG are group-wise features. The paper proposes dividing feature channels into groups and then separately normalizing all channels within each group.
All normalization layers can be defined by the following computation.

where μi and σi are mean and standard deviation

Si is the set of indexes across which the mean and standard deviation are calculated for index i. m is the size of the set Si which is the same for all i.
The definition of Si is different for Batch normalization, Layer normalization, and Instance normalization.
Batch Normalization
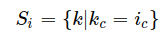
The values that share the same feature channel are normalized together.
Layer Normalization

The values from the same sample in the batch are normalized together.
Instance Normalization

The values from the same sample and same feature channel are normalized together.
Group Normalization
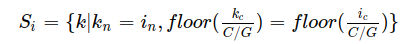
where G is the number of groups and C is the number of channels.
Group normalization normalizes values of the same sample and the same group of channels together.
class GroupNormalization(L.Layer):
def __init__(self, groups, channels, eps=1e-5, **kwargs):
super().__init__(**kwargs)
self.eps = eps
self.groups = groups
self.channels = channels
self.scale = self.add_weight(shape=channels, initializer='zeros', trainable=True)
self.shift = self.add_weight(shape=channels, initializer='ones', trainable=True)
def call(self, x):
x_shape = x.shape
batch_size = x_shape[0]
x = tf.reshape(x, (batch_size, -1, self.groups))
mean = tf.reduce_mean(x, [1], keepdims=True)
mean_x2 = tf.reduce_mean((x ** 2), [1], keepdims=True)
var = mean_x2 - mean ** 2
x_norm = (x - mean) / tf.sqrt(var + self.eps)
x_norm = tf.reshape(x_norm, (batch_size, -1, self.channels))
x_norm = tf.reshape(self.scale, (1, 1, -1)) * x_norm +tf.reshape(self.shift, (1, 1, -1))
return tf.reshape(x_norm, x_shape) Weight Standardization
Batch Normalization doesn’t work well when the batch size is too small, which happens when training large networks because of device memory limitations. The paper Micro-Batch Training with Batch-Channel Normalization and Weight Standardization introduces Weight Standardization with Batch-Channel Normalization as a better alternative.

for a 2D-convolution layer O is the number of output channels and I is the number of input channels times the kernel size (I=C_in×K_H×K_W)
def weight_standardization(weight):
c_out, c_in, *kernel_shape = weight.shape
weight = tf.reshape(weight, (c_out, -1))
mean = tf.reduce_mean(weight, [1], keepdims=True)
mean_x2 = tf.reduce_mean((weight ** 2), [1], keepdims=True)
var = mean_x2 - mean ** 2
weight = (weight - mean) / (tf.sqrt(var + eps))
return tf.reshape(weight, (c_out, c_in, *kernel_shape)) Batch-Channel Normalization
This first performs a batch normalization. Then a channel normalization is performed.
Channel Normalization is similar to Group Normalization but affine transform is done group wise.
class ChannelNormalization(L.Layer):
def __init__(self, groups, channels, eps=1e-5, **kwargs):
super().__init__(**kwargs)
self.eps = eps
self.groups = groups
self.channels = channels
self.scale = self.add_weight(shape=groups, initializer='zeros', trainable=True)
self.shift = self.add_weight(shape=groups, initializer='ones', trainable=True)
def call(self, x):
x_shape = x.shape
batch_size = x_shape[0]
x = tf.reshape(x, (batch_size, -1, self.groups))
mean = tf.reduce_mean(x, [1], keepdims=True)
mean_x2 = tf.reduce_mean((x ** 2), [1], keepdims=True)
var = mean_x2 - mean ** 2
x_norm = (x - mean) / tf.sqrt(var + self.eps)
x_norm = tf.reshape(self.scale, (1, 1, -1)) * x_norm +tf.reshape(self.shift, (1, 1, -1))
return tf.reshape(x_norm, x_shape) References
Hungry for more insights?
Don’t miss out on exploring other fascinating threads in this series. Simply click here and uncover the state-of-the-art research!
Do Subscribe for weekly updates!!